Pierwszym sposobem zmniejszania liczby stanów układu było upraszczanie. Dzisiaj napiszę o drugim ze sposobów, jakim jest partycjonowanie.
Gra w kości
Aby zrozumieć czym jest partycjonowanie i jak wpływa na złożoność, posłużymy się kostkami do gry. Weźmy układ złożony z dwóch kostek sześciościennych. Taki układ ma 36 możliwych stanów, w których może się znaleźć. Jeśli jednak jedną kostką będziemy rzucać oddzielnie od drugiej, to taki układ dwóch niezależnych od siebie układów jedno-kostkowych będzie już miał jedynie 6 + 6 = 12 możliwych stanów.Inny przykład: dla układu 3 kostek liczba możliwych stanów, w których może się on znaleźć wynosi 216. Jednak jeśli ten układ podzielimy na 3 oddzielne i niezależne układy jedno-kostkowe, to liczba stanów takiego układu będzie wynosiła 6 + 6 + 6 = 18.
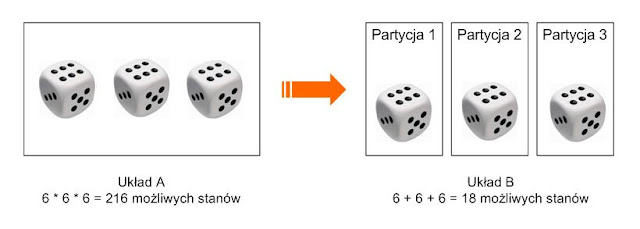 |
| Spartycjonowanie układu 3 kostek. Źródło: R. Sessions. |
Uogólniając - dla układu B niezależnych układów kostek, z których każdy zawiera D kostek F-ściennych, liczba możliwych stanów, czyli całkowita złożoność C takiego układu układów kostek, będzie wyrażona wzorem:
C = B * F^D
Jeśli układ 12 kostek podzielimy na dwa oddzielne, niezależne układy, każdy złożony z 6. kostek, to liczba stanów takie układu układów będzie wynosiła 2 * 6^6 = 93.000 stanów. Innymi słowy podzielenie układu 12 kostek na dwa niezależne układy sześciu kostek zmniejszyło nam złożoność całego układu z ponad dwóch miliardów do około 96.000, co daje 99,99571 procentowe zmniejszenie złożoności! Podział układu 12 kostek na 3 niezależne części zmienia złożoność układu z ponad dwóch miliardów stanów do 3 * 6^4 = 3.888 stanów, co daje pod 500.000-krotne zmniejszenie złożoności.
Partycjonowanie
Podział układu kostek na niezależne podukłady zmniejsza istotnie złożoność takiego układu pod jednym ważnym założeniem - każda kostka musi się znaleźć w dokładnie jednym podukładzie (nie może występować w kilku). Istnieje w matematyce analogiczna koncepcja dzielenia przestrzeni elementów na grupy - to podział (partycja) zbioru. Podział zbioru X, to zbiór P niepustych podzbiorów zbioru X takich, że każdy element x zbioru X znajduje się w dokładnie jednym podzbiorze zbioru P . W efekcie suma elementów wszystkich takich podzbiorów powinna dawać zbiór X a dla każdej pary różnych podzbiorów ich część wspólna jest zawsze zbiorem pustym:Przy założeniu, że układ kostek, system informatyczny oraz proces biznesowy są ze sobą homomorficzne, podział (spartycjonowanie) układu kostek, systemu informatycznego lub procesu biznesowego istotnie zmniejszy ich złożoność.
Poniższy rysunek przedstawia model zmniejszania złożoności systemów informatycznych za pomocą partycjonowania.
 |
| Model zmniejszania złożoności architektury IT za pomocą partycjonowania. Opracowanie własne. |
Po lewej stronie rysunku widać cztery systemy A, B, C i D, połączone każdy z każdym. Każdy z nich ma (średnio) po 10 istotnych stanów kontrolowanych przez jego zmienne. W takim układzie analityk podczas analizy lub tester podczas testowania widzi i analizuje lub testuje na raz, jako jedną całość, układ 4 systemów o łącznej złożoności 10^4 = 10.000 stanów.
Aby zmniejszyć złożoność takiego układu, dzielimy go na dwie części w taki sposób, aby jeden system znalazł się dokładnie w jednej z części (partycji). I tak systemy A i B trafiają do partycji AB a systemy C i D trafiają do partycji CD. W celu zachowania zależności pomiędzy systemami wchodzącymi w skład obu partycji, partycja AB wystawia partycji CD usługi niezbędne do działania systemów C i D a partycja CD wystawia partycji AB usługi niezbędne do działania systemów A i B. Te dwa zbiory usług ukrywają wewnętrzną złożoność systemów je realizujących, więc można traktować je jako prostsze systemy. W przykładzie przyjęto, że złożoność takiego zbioru usług będzie również wynosiła 10 stanów - tak, jak dla każdego innego z systemów w całym układzie. Ale dla zbioru usług ukrywających złożoność realizujących je systemów można przyjąć dowolną inną liczbę stanów mniejszą od złożoności systemów ukrywanych pod tymi usługami.
W układzie podzielonym (po prawej stronie ww. rysunku) widać dwie partycje. Partycja AB jest zbudowana z systemów A i B oraz z zestawu usług świadczonych przez partycję CD i niezbędnych do działania systemów partycji AB. Partycja CD jest zbudowana z systemów C i D oraz z zestawu usług świadczonych przez partycję AB i niezbędnych do działania systemów partycji CD. W takim układzie analityk podczas analizy lub tester podczas testowania widzi i analizuje / testuje na raz, jako jedną całość, układ 2 systemów i jednego zestawu usług o łącznej złożoności 10^3 = 1.000 stanów. A ponieważ w układzie istnieją dwie takie części do analizy lub testowania, każda o złożoności 1.000 stanów, to całkowita złożoność takiego układu będzie wynosiła 1.000 + 1.000 = 2.000 stanów. W wyniku partycjonowania zmniejszyliśmy więc złożoność układu z o 80% - z 10.000 do 2.000 stanów.
Zakończenie
Widać, że podział zbioru systemów na części pozwala na istotne zmniejszenie złożoności całego układu. Dodatkowo, im więcej części wydzielimy, tym zmniejszenie złożoności będzie większe. W przedstawionym przykładzie partycjonowania systemów, wyjściowym układem był układ czterech systemów, które podzielono na 2 partycje. Ponieważ systemy były połączone każdy z każdym, to wybór systemów do poszczególnych partycji mógł być dowolny.W rzeczywistości jednak takie sytuacje nie zdarzają się nigdy. Dlatego zasadniczym wyzwaniem przy partycjonowaniu systemów staje się wybór takiego sposobu ich podziału, który będzie uwzględniał faktyczne istniejące zależności pomiędzy tymi systemami (dokładniej: pomiędzy funkcjonalnościami tych systemów) i będzie generował maksymalną możliwą liczbę partycji o jak największej liczbie / sile zależności między funkcjonalnościami partycji oraz o jak najmniejszej liczbie / sile zależności między funkcjonalnościami różnych partycji. Wtedy złożoność interfejsów wystawianych przez jedną partycję i używanych w innych, będzie najmniejsza a tym samym złożoność samych partycji będzie najmniejsza a tym samym złożoność całego układu będzie najmniejsza.
Z pomocą w poszukiwaniu takiego sposobu podziału funkcjonalności pomiędzy systemy, aby złożoność całości była jak najmniejsza, przychodzi relacja równoważności. Ale o tym w następnym odcinku.
Bibliografia
- Partition of a set, http://en.wikipedia.org/wiki/Partition_of_a_set, [2012-07-13].
- Sessions R., A Better Path to Enterprise Architecture, marzec 2006, ObjectWatch, http://www.objectwatch.com/whitepapers/ABetterPath-Final.pdf, [2012-08-19].
- Sessions R., Simple Architectures for Complex Enterprises, 1 edycja kindle 2010, Microsoft Press.
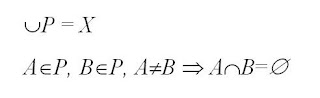
Brak komentarzy:
Prześlij komentarz